更新:已报名的队伍可以通过链接查询账号密码啦:https://www.wjx.cn/resultquery.aspx?activity=124013137
如标题所说,在去年的第一届美团杯大获成功之后,第二届美团杯终于来啦!
本次比赛的报名将于今天开始,至 2021 年 7 月 4 日周日中午 12:00 截止,具体报名方式见下方正文。正式比赛的时间为 2021 年 7 月 11 日下午 13:00 至晚上 18:00。希望大家多多来捧场。
本次比赛由北京大学学生算法协会与美团共同主办。非常感谢美团对我们再次的支持!同时比赛的平台会放在 UOJ 上,感谢吕凯风老师在百忙之中仍然抽时间给我们的比赛提供帮助!
想碎碎念的大概就是这些,接下来是正文部分,也就是关于这场比赛的介绍~ 因为我自己不怎么会排版,所以这儿就只放文字部分了。包含图片的版本可以移步我社的公众号 PKUSAA。
赛事简介
“美团杯”程序设计挑战赛是由北京大学学生算法协会 & 美团主办的高质量程序设计竞赛,面向所有对计算机编程、算法感兴趣的大学生、中小学生及社会人士,旨在为编程爱好者们提供一个高水准兼具趣味性与挑战性的竞赛平台,来展示自己分析解决问题、快速吸收新知识的能力。作为专业的程序设计竞赛,本次比赛由国内外算法竞赛顶尖选手负责命题,由北京大学教授担任赛事顾问,以确保比赛的高质量与专业性。同时,北京大学学生算法协会也希望能够以此赛事为平台,在传统算法竞赛的基础上探索更多的题目类型与比赛形式,为算法竞赛的发展注入新的活力。
比赛赛制
比赛采用类IPSC赛制。
- 参赛选手至多三人一队,并以队伍为单位进行比赛。
- 比赛时长5个小时,包含10-13道正式赛题和1道热身题。热身题将在下方给出,正式赛题在比赛开始后才会开放。
- 正式比赛的最后一小时会封榜,在这个时候,所有队伍只能看到自己的提交结果,但是无法看到别的队伍的分数变化。
- 每一道正式赛题包含small和large两个独立部分,其中small占35分,large占65分,即一道正式赛题总分100分;热身题只有一个部分,不占分。对于选手的每一次提交,评测机都会分别对small和large进行检查,并按照情况给出0, 35, 65, 100分中的某一个分数。注意:只有在同一次提交中同时通过了small和large,才能获得100分;如果在两次不同的提交中分别通过了small和large,得分将被判定为 65 分。
- 队伍排名按照总得分降序排序,对于得分相同的队伍,按照罚时升序排序。罚时的计算方式如下:
- 每一道正式赛题的罚时等于最高分提交的时间(如有多个提交得分相同取最前面的那个)加上错误提交次数乘以 20 分钟。错误提交次数定义为:最高分提交之前的提交次数扣除掉第一次得分为 35 的提交、第一次得分为 65 的提交以及所有编译不通过的提交。
- 热身题的罚时等于负二十分钟,即通过热身题可以减免二十分钟的罚时。
- 一个队伍的罚时等于所有通过的部分的罚时之和。
奖项设置
获奖队伍的所有成员须均为在校学生(包括中小学、大学本专科及全日制硕士、博士研究生,含本年度应届毕业生),其余队伍不计入最终评奖。
- 一等奖:冠军队伍 3000RMB/人
- 二等奖:两支队伍 1500RMB/人
- 三等奖:三支队伍 1000RMB/人
- 优胜奖:九支队伍
- 最快解题奖:最快通过某一道正式赛题的large部分的队伍
- 顽强拼搏奖:比赛结束前最后通过某一道正式赛题的某个部分的队伍
- 阳光普照奖:从得分不为0且没有获得以上奖项的队伍中随机抽取五支队伍
后四个奖项的获奖队伍将获得由美团提供的精美定制礼品,奖品会在后续通知中公开。
在评奖过程中,所有有获奖资格的队伍会被分为两组:大学生组(所有成员均为大学本专科及全日制硕士、博士研究生的队伍)以及中小学生组(存在成员为中小学生的队伍,包括21年9月即将升学的高中生以及大学预科生):我们会保证大学生组至少有一支队伍获得二等奖及以上奖项,至少有三支队伍获得三等奖及以上奖项,以及至少有九支队伍获得优胜奖及以上奖项。
赛事流程
- 注册报名:即日起-7月4日中午12:00内填写下方问卷报名
- 加入交流群:北大算协&美团比赛交流群(入群方式见问卷末尾)
- 积极备赛:尝试并解决热身题
- 测试赛:7月9日晚上19:30-20:30
- 比赛时间:7月11日中午13:00-18:00
- 赛后交流:7月11日晚上20:00,由命题组直播进行题目讲解
- 获奖名单揭晓:7月13日中午12:00
指导与出题人
本次赛事邀请了北京大学的罗国杰教授和张勤健老师作为赛事顾问。
同时我们也邀请到了杜瑜皓、金策、周雨扬、The NANO团队以及其他很多不愿透露姓名的优秀出题人们来为这场比赛命题。
热身题
本次比赛的热身题是一道数回。作为热身题,欢迎大家在赛前讨论、并尝试用各种方式解决它。
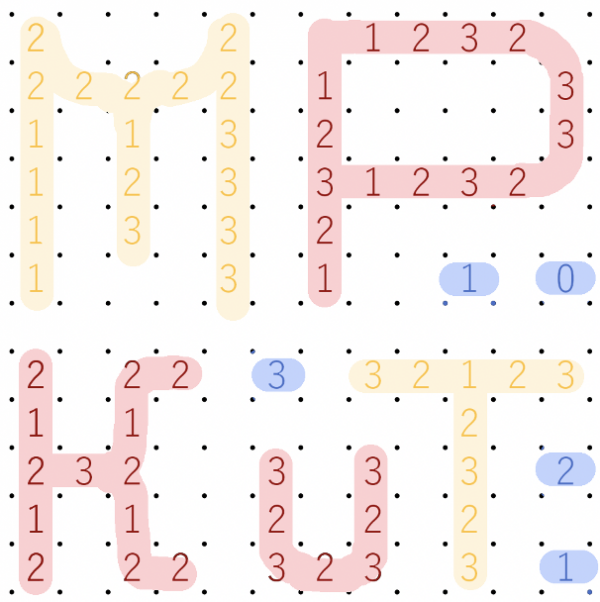
规则:
- 你需要在网格的格点之间用直线和横线相连,使得你连上的所有线恰好构成了一个不间断、不分叉的回路。
- 网格中存在一些 0~3 之间的数字,表示这个格子四周划线的数量。
- 对于没有数字的格子,周围的划线数目没有任何限制。
下图是一个数回的简单的例子:
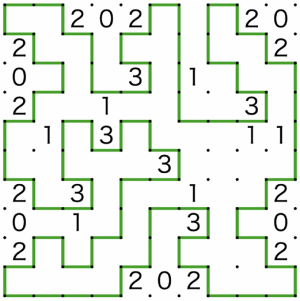
在正式比赛开始后,热身题的提交将会开放。提交格式如下:
- 你需要提交 $25$ 行数据,每行包含一个 $01$ 串,其中 $1$ 表示连线,$0$ 表示没有连。
- 数据的前 $13$ 行形成了一个 $13\times12$ 的 $01$ 矩阵,按照从上到下从左到右的顺序描述了每一条横线是否被连。
- 数据的后 $12$ 行形成了 $12\times 13$ 的 $01$ 矩阵,按照从上到下从左到右的顺序描述了每一条竖线是否被连。
选手须知
本赛事秉承公平公正的原则,严厉查处作弊行为。参赛选手需遵守选手须知,每支队伍独立完成比赛。在比赛结束后,我们会通过代码查重等方式来检测作弊行为,并取消作弊队伍的评奖资格。参赛选手应当认真阅读下述选手须知,一旦报名成功,默认参赛者接受并承诺遵守相关规定。
- 正式比赛过程中允许同一个队伍的多名选手同时进行解题,并允许选手自由使用各类辅助工具、互联网上的教程信息。
- 正式比赛过程中所有赛题相关的讨论只能在队伍内部进行。
- 比赛过程中禁止对评测系统作任何形式的攻击行为。
- 在比赛结束后的30分钟内,选手需要整理所有正式赛题相关的解题材料(包括代码、草稿等)并以指定的方式上传,以作为作弊处理工作的参考。
- 本次比赛的赞助商有权获得参赛者的报名资料。
- 北京大学学生算法协会对赛制保留最终解释权。
报名方式
扫描下方二维码或者点击此处填写表单,提交成功即视为报名成功。工作人员会在2021年7月7日之前对报名情况进行审核,并在审核通过后和您联系。
期待您的加入!

常见问题
Q:好感兴趣,怎么报名本次比赛呀?
A: 在本页最下方,扫描二维码,填写问卷信息提交报名即可。本次比赛以队伍为单位进行报名,一个队伍最多包含三名队员,当然我们也欢迎单人队伍与双人队伍的参加。
Q: 想和同学们在线讨论,可有组织收留?
A: 欢迎加入官方交流群“北大算协&美团比赛交流群”(入群方式见问卷末尾),如遇问题可以在群里进行讨论或者发送邮件至北京大学学生算法协会(pkusaa@yeah.net)
Q: 想和来自不同学校的朋友一起参赛,可以吗?
A: 本次比赛的队伍没有学校的限制,欢迎呼朋唤友参加赛事。如果希望深入交流,可以加入“北大算协&美团比赛交流群”(入群方式见问卷末尾)。
Q: 已经报名,想好好学习备赛,有推荐资源吗?
A: 本次比赛在传统算法竞赛的基础上,会包含形式更加灵活的题目。如果对算法竞赛的知识感兴趣,可以访问OI Wiki;如果想要练习多样化的题目,可以尝试一下往年IPSC的赛题。也非常欢迎来做一做去年美团杯的题目练练手~
Q: 还有其他问题想问,怎么咨询?
A: 加入官方QQ交流群(入群方式见问卷末尾),可以直接在群内咨询。
本次活动最终解释权归北大算协所有
赞助商信息
本次活动由美团独家赞助。

美团的使命是“帮大家吃得更好,生活更好”。作为一家生活服务电子商务平台,公司聚焦“Food +Platform”战略,以“吃”为核心,通过科技创新,和广大商户与各类合作伙伴一起,努力为消费者提供品质生活,推动生活服务业需求侧和供给侧数字化升级。2018年9月20日,美团正式在港交所挂牌上市。美团将始终坚持以客户为中心,不断加大在科技研发方面的投入,更好承担社会责任,更多创造社会价值,与广大合作伙伴一起发展共赢。


 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号